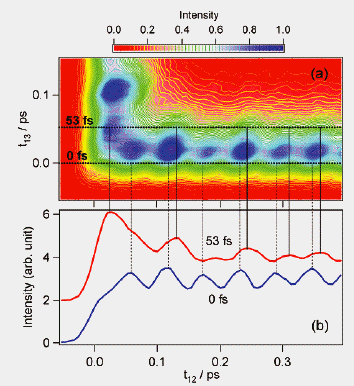
図1. 色素オキサジン4をポリビニルアルコール(PVA)のフィルムにドープし、その縮退4光波混合信号の測定を10 Kで行ないました。
(a)は縮退4光波混合の信号強度をt12とt13に対して、等高線プロットしたものです。青い部分で信号が強く、赤い部分では弱くなっています。
(b)はt13=0と53 fsでの信号強度のt12依存性を抜き出したものです。((a)の横軸方向の断面図)すると、信号に現れてるコヒーレントな振動の様子がt13=0と53 fsで違うことがわかりました。
フォトンエコーの論文がようやくまた一報出ました!
4年生だった森芳雄君ががんばって実験してくれたおかげです。
卒業してから2年以上経ってやっと論文になりました…(あ〜、たいへんだった。)
フォトンエコーとは過渡回折格子(transient grating: TG)と同様な縮退4光波混合の一種です。過渡回折格子はレーザーパルスの電場同士の干渉によって生じた干渉縞により、3つ目のパルスがブラッグ回折されることによって信号が発生します。そこで、1つ目と2つ目のパルスが同時(t12=0)に来ないと、信号が発生しません。これに対し、フォトンエコーは1つ目のパルスによってサンプルに生じた分極と、2つ目のパルスの電場の干渉によって起こるので、パルスが同時に来なくても信号が発生します。そこで、この特性を利用して新しいコヒーレント振動分光法が開発できないか?と当研究室では考えました。

図1. 色素オキサジン4をポリビニルアルコール(PVA)のフィルムにドープし、その縮退4光波混合信号の測定を10 Kで行ないました。
(a)は縮退4光波混合の信号強度をt12とt13に対して、等高線プロットしたものです。青い部分で信号が強く、赤い部分では弱くなっています。
(b)はt13=0と53 fsでの信号強度のt12依存性を抜き出したものです。((a)の横軸方向の断面図)すると、信号に現れてるコヒーレントな振動の様子がt13=0と53
fsで違うことがわかりました。
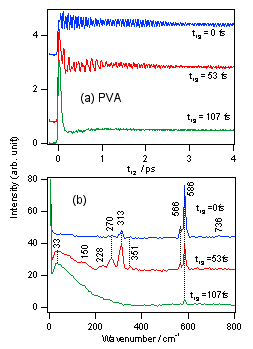
図2 (a) t12の範囲を長く取ると、違いがより明確になります。t13=0の方が53
fsより高波数で振動しているように見えます。さらにt13=107 fsまで長くすると、振動は非常に弱くなり、時間原点付近にスパイクのような超高速の減衰が現れ、一旦減衰した信号が若干回復している様子がわかります。
(b) これらの信号をフーリエ変換したものの実数部のスペクトルです。t13=0では、585cm-1付近に強いバンドが現れており、310cm-1付近に弱いバンドがあることがわかります。これがt13=53
fsになると、310cm-1付近のバンドが強くなっており、t13=0でははっきり見えなかったバンドも見えるようになっていることがわかります。さらに30
cm-1に非常にブロードな低波数バンドが現れていることがわかります。
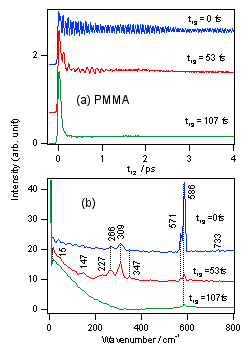
図3 (a)、(b) 同様な実験をPMMAにドープした場合について行なっても、同様な結果が得られました。特に147、227、347cm-1のような非常に弱いバンドについても再現性があることに注目して下さい。
これらの実験結果を最初に学会で発表した時に、理研の田原さんに「2つのパルスが時間的にずれるのは、パルス幅が広がるのと同様のことであり、波数領域において「観測窓」が低波数側に狭まっているだけではないか」との指摘を受けました。
しかし、パルス幅が広がることにより「観測窓」が狭まっているのであれば、高波数側から単調にバンド強度が弱くなっていくはずです。この実験の場合、実際に低波数バンドの強度が強くなっているので、単なる「観測窓」効果ではないことがわかります。

図4 (a) 室温のオキサジン4/メタノール溶液のポンプ・プローブ信号です。コヒーレントな振動が現れているのがわかります。
(b)はこの信号のフーリエ変換スペクトルの実数部です。277、306cm-1に弱いバンドが現れていますが、それ以外のバンドは見えません。このことからも、低温のエコー信号ではいくつかの低波数バンドが増幅され、室温のポンプ・プローブ信号では見えない信号が現れていることがわかります。
なぜこのような増幅現象が起こるのでしょうか?
その原因を解明するためコンピューターシミュレーションを行ないました。

図5 (a) フォトンエコー信号の10 Kから240 Kまでの温度変化です。
(b) 温度変化のシミュレーションです。こうしてフィッテングパラメータの値を決定していきます。

図6 ついでに室温におけるオキサジン4の吸収スペクトルのフィッテイングも行ないました。だいたい合ったので、これで良しとしました。
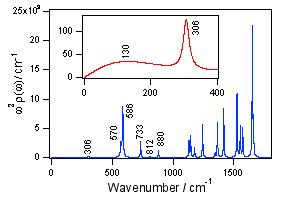
図7 フィッテイング得られたスペクトル密度です。130 cm-1にピークのある非常に弱いバンドはフィルムのフォノンモードであり、ブラウン振動子で近似してあります。それ以外のバンドはオキサジン4の分子内振動であり、共鳴ラマンスペクトルから得られたパラメータを使用してあります。
こうして得られたパラメータを用いて、図1〜3の結果を再現できるか、シミュレーションしてみました。
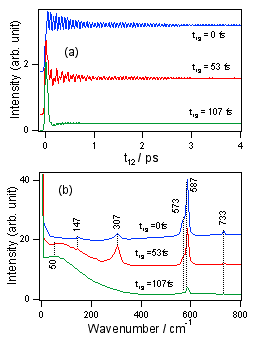
図8 (a)、(b) シミュレーションの結果です。実験結果を極めて良く再現していると言えます。300cm-1付近には、307cm-1に一本しかバンドが現れていませんが、これはシミュレーションに用いたラマンスペクトルには、これ以外のデータが得られていなかったからです。
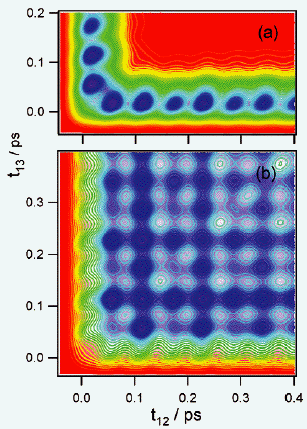
図9 (a) シミュレーションで得られた縮退4光波混合信号の等高線プロットです。
凝縮相での電子状態の位相緩和は10 Kでも非常に速く、フォトンエコーは超高速で減衰してしまいます。位相緩和を遅くすることができれば、コヒーレント振動について、より詳細な研究ができるのですが、実際の実験でこれは困難です。しかし、シミュレーションでは簡単に位相緩和を遅くすることができます。位相緩和の原因であるフォノンモードを取り除いてやればいいのです。
(b) フォノンモードを取り除いて行なった同様のシミュレーションです。フォトンエコー信号が広範囲にわたって出現しているのがわかります。
そこで、この信号の断面図を詳しく解析してみましょう。

図10 (a) 様々なt13の値における図9 (b)の断面図です。
(b) そのフーリエ変換信号です。
307cm-1のバンドが53 fsおきに強くなったり弱くなったりしていることがわかります。
53 fsというのは、307cm-1のバンドの約半周期に相当します。
このような現象は587cm-1のバンドについては、観測されませんでした。
また、50cm-1のバンドは現れていません。この低波数のブロードなバンドはフォノンモード由来であることがわかります。

図11 (a) 307cm-1以外の800m-1以下のバンドを取り除いて行なった同様のシミュレーション。t13の値を53
fsずつ増加させて信号をシミュレーションしました。位相が半周期ずれている時に振幅が最大になることがわかります。
(b) 587cm-1以外の800m-1以下のバンドを取り除いて行なった同様のシミュレーション。23
fsごとにt13を増加させてみましたが、307cm-1の場合のような現象は起こりません。
587cm-1のバンドは、307cm-1のバンドに比べて、高波数にあるというだけでなく、その再配向エネルギーも高いことが共鳴ラマンの実験からわかっています。587cm-1のバンドの再配向エネルギーは188
cm-1あり、307cm-1のバンドのそれ(11 cm-1)よりも約15倍大きな値をしています。
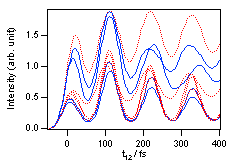
図12 そこで、307cm-1以外の800m-1以下のバンドを取り除き、307cm-1のバンドの再配向エネルギーの値を188
cm-1に増加させて、同様のシミュレーションを行ないました。この場合も、t13の値を53
fsずつ増加させて信号をシミュレーションしましたが、はっきりとした増幅効果はもはや見られません。
増幅効果は低波数で再配向エネルギーの小さなバンドにのみ現れるということがわかりました。
では、なぜこのようなことが起こるのでしょうか?
フォトンエコーには昔から「モード抑制」という効果があることが知られていました。
フォトンエコーで超高速の電子状態の位相緩和時間を測定しようとすると、信号にコヒーレント振動が乗ってしまい、どうしても正確な緩和時間が測定できませんでした。そこで、「モード抑制」という効果を利用してコヒーレント振動の影響を最小限に抑制しようというテクニックです。
簡単な近似のもとで、フォトンエコー信号は以下のような式で表すことができます。
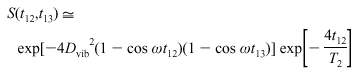
ここでωは分子振動の角振動数ですが、t13の値をちょうどその振動周期の整数倍にすると、1-cos2nπ=0となり、振動の寄与は消えてしまいます。逆にt13の値を(振動周期の整数倍+半周期)にすると1-cos(2n+1)π=2となり、振動の寄与は最大になります。
ところで、過渡回折格子はt13=0なので、n=0の場合に相当し、モード抑制がかかっていることになります。
当然、(振動周期の整数倍+半周期)の場合のフォトンエコーの方が振動の寄与は強くなります。
今まで、振動の抑制は知られていたのですが、その増幅は知られていなかったのです。
ちゃんちゃん。
(クソ難しい話をだいぶはしょって書いたので、これ読んでわかる人ほとんどいないと思われ…。ま、いいっか。)